Как рассчитать чистый дисконтированный доход (формула)

Чистый дисконтированный доход — показатель, позволяющий оценить инвестиционную привлекательность проекта. Основываясь на величине чистого дисконтированного дохода, инвестор может понять, насколько обоснованными являются его первоначальные капиталовложения с учетом запланированного уровня доходности проекта, не дожидаясь его завершения.
Чистый дисконтированный доход: формула
В общем порядке величина чистого дисконтированного дохода определяется как сумма всех дисконтированных значений потоков будущих платежей, приведенных к сегодняшнему дню, и определяется следующим образом:
NPV = – IC + Ʃ CFt/ (1 + r)ᵗ,
NPV — величина чистого дисконтированного дохода;
IC — первоначальные инвестиции;
CFt — потоки денежных средств в конкретный период срока окупаемости проекта, которые представляют собой суммы притоков и оттоков денежных средств в каждом конкретном периоде t (t = 1. n);
r — ставка дисконтирования.
В зависимости от значения данного показателя инвестор оценивает привлекательность проекта. В случае, если:
1. NPV > 0, то инвестиционный проект выгоден, инвестор получит прибыль;
2. NPV = 0, то проект не принесет ни прибыли, ни убытка;
Также для анализа инвестиционной привлекательности проекта инвесты изучают чистый денежный поток предприятия. Существует 2 метода определения величины чистого денежного потока: прямой и косвенный.
Денежный поток рассчитывается по специальной формуле, которую можно найти в материале от КонсультантПлюс. Если у вас нет доступа к системе К+, получите пробный онлайн-доступ бесплатно.
Учет инфляции при расчете чистого дисконтированного дохода
В связи с тем, что в некоторых ситуациях инфляционные колебания невозможно нивелировать на практике, возникает вопрос о том, каким образом отразить влияние инфляции на показатель чистого дисконтированного дохода. Наиболее распространенным решением данной проблемы является корректировка дисконта на прогнозируемый уровень инфляции.
При этом процентная ставка будет рассчитываться следующим образом:
R — дисконтная ставка с учетом инфляции;
J — уровень инфляции.
Таким образом, чем выше уровень инфляции, прогнозируемый на время реализации проекта, тем ниже должна быть доходность проекта, чтобы после дисконтирования проект не стал убыточным.
Чистый дисконтированный доход: пример расчета
Предположим, что инвестор хочет модернизировать систему автоматизации производственного процесса. Предполагается, что сумма затрат на перевооружение конвейера составит 50 000,00 руб. При этом планируется увеличение объемов производства за счет нового оборудования, как следствие — увеличение объемов продаж в течение ближайших 5 лет. Приток денежных средств за 1-й год составит 45 000,00 руб., за 2-й год — 40 000,00 руб., за 3-й год — 35 000,00 руб., за 4-й год — 30 000,00 руб., за 5-й год — 25 000,00 руб. Необходимая норма прибыли — 10%. Расчет приведенной стоимости проекта представлен в таблице.
Ставка дисконтирования: что это, где применить и как рассчитать

Ставка дисконтирования — это эталонная величина, выраженная в процентах, применяемая для сравнительной оценки эффективности инвестиций.
Например, вам нужно выбрать: положить деньги в банк со ставкой депозита 12% сроком на пять лет с ежегодной выплатой процента или купить облигации с погашением через девять лет с купоном 8,5%, выплачиваемым дважды в год и с текущей ценой 91% от номинала. Как вы будете выбирать, да еще учитывая, что уровень инфляции составляет около 8%?

Для решения этих задач используется прием, который называют дисконтированием. С помощью дисконтирования можно сопоставить будущие денежные потоки и выбрать из нескольких вариантов инвестиций самый выгодный. А ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.
Правильный расчет ставки дисконтирования позволит вам:
- оценить эффективность инвестиций относительно надежных вкладов;
- сравнить варианты инвестиций с разной длительностью вложения;
- сравнивать доходность вложений инструментов с разной степенью риска.
Ставка дисконтирования зависит от множества факторов: уровень инфляции, доступные для инвестора варианты вложений, риск вложений, стоимость вашего капитала и др. Но далеко не все внешние факторы можно достоверно учесть в ставке.
Как появилась ставка дисконтирования
Первоначально ставка дисконтирования применялась при учете векселей. Принимая к оплате вексель, банкиры знали сумму, которую они получат, когда предъявят вексель к погашению. Но чтобы им самим заработать, банкиры выплачивали предъявителю деньги со скидкой — дисконтом. А процентная ставка, в которой измерялся их доход, называлась учетной ставкой, или ставкой дисконтирования (discount rate). Сумма, которая выплачивалась предъявителю векселя, рассчитывалась как раз с помощью дисконтирования — зная, сколько он получит в будущем и учитывая текущий уровень процентных ставок, банкир определял текущую стоимость денег.
Этот прием оказался настолько универсальным и полезным, что стал широко применяться при оценке и сравнении эффективности вложений в разные инструменты или проекты. При дисконтировании инвестор, как и банкир при учете векселей, пересчитывает стоимость денег, которые он получит в будущем, причем в совершенно разные сроки, на текущую стоимость. Он как бы проецирует стоимость денег из будущего на плоскость настоящего времени. А центральным звеном расчетов выступает ставка дисконтирования.

Как рассчитать ставку дисконтирования
При расчете ставки дисконтирования очень важно определить ставку, которая позволит максимально корректно привести будущую стоимость доходов и расходов к текущей. Для этого нужно учитывать и общий уровень процентных ставок, и факторы риска вложений в отдельные инструменты.
При расчете ставки дисконтирования нужно учесть два основных вида факторов:
- Уровень безрисковых ставок.
- Премии за риск.
Безрисковые ставки — это процентные ставки инструментов с минимальным для инвестора уровнем риска. Обычно такими инструментами являются облигации центрального правительства — ОФЗ в России, US Treasuries в США и т. п. Также в качестве безрисковых ставок могут учитываться ставки по депозитам системообразующих банков. Иногда как безрисковая ставка может рассматриваться ключевая ставка центральных банков.
Уровень безрисковых ставок является фундаментальным — он определяет минимальный уровень всех ставок дисконтирования.
Премии за риск — это надбавки к уровню безрисковых ставок, которые стоит учитывать при вложении в отдельные инструменты или проекты. Это могут быть общие факторы — уровень инфляции, надбавка за страновой риск; факторы, учитывающие риск вложения в отдельные инструменты, — надбавка за отраслевой риск, надбавка за индивидуальный риск (зависит от надежности эмитента, инструмента или проекта).
Учет премий за риск позволит более точно настроить инструмент дисконтирования, чтобы избежать ошибок в сравнении разных инвестиций.
При расчете ставки дисконтирования используются различные способы и методы, которые можно объединить в такие основные группы:
- интуитивные методы;
- модели на основе премий за риск;
- аналитические модели.
Интуитивные методы
В эту группу включается:
- собственно интуитивный метод.
- экспертный метод.
Интуитивный метод — это способ определения ставки дисконтирования на основе субъективного видения инвестора. Проще говоря, когда инвестор прикидывает ставку дисконтирования практически на глазок. Например, он рассуждает так: «Я могу положить деньги на депозит в надежном банке под 12–15%. Тогда эффективность других вложений я буду сравнивать с таким уровнем ставок».
Экспертный метод — это, по сути, тот же интуитивный метод, только итоговая величина ставки дисконтирования выводится как совокупный консенсус нескольких экспертов с тем или иным уровнем обоснованности их мнений.

Модели на основе премий за риск
К моделям на основе премий за риск относятся, например, такие модели, как:
- модель кумулятивного построения;
- модель капитальных активов CAPM.
Общим для этих моделей является то, что ставка дисконтирования выводится как сумма безрисковой ставки и премий за риск.
Модели кумулятивного построения — это метод определения ставки дисконтирования, при котором к безрисковой процентной ставке прибавляются все премии за риск, которые можно определить для конкретного инструмента.
Формула расчета ставки дисконтирования кумулятивным способом выглядит так:
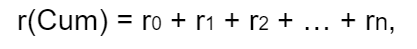
где r 0 — безрисковая ставка,
r 1 , r 2 , r n — все премии за риск для оцениваемого инструмента.
Модель капитальных активов CAPM (Capital Asset Pricing Model, модель оценки капитальных активов) — это метод определения ставки дисконтирования для сравнительной оценки эффективности вложений в акции, при котором к безрисковой процентной ставке прибавляется премия за риск по отдельному инструменту с учетом его β-коэффициента.
β-коэффициент (бета-коэффициент) — это мера рыночного риска акции, которая показывает изменчивость доходности акции к доходности на рынке в среднем. β-коэффициент численно показывает, на сколько процентов изменяется цена акции бумаги при росте или снижении индекса на 1%. Положительный коэффициент говорит о том, что акция двигается в одном направлении с рынком, а отрицательный коэффициент означает, что акция двигается в противоположную от общего направления рынка сторону.
β-коэффициенты рассчитываются и публикуются и аналитиками, и торговыми площадками, например Московской биржей.
Формула расчета ставки дисконтирования по CAPM выглядит так:
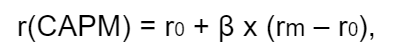
где r 0 — безрисковая ставка,
r f — средняя доходность фондового рынка (биржевого индекса).

Аналитические методы
Аналитические методы — способы расчета ставки дисконтирования с применением элементов финансового анализа. Среди аналитических методов можно выделить:
- WACC;
- мультипликативные методы.
WACC — это средневзвешенная стоимость капитала (Weighted Average Cost of Capital). WACC используется компаниями для сравнительной оценки эффективности инвестиционных проектов.
Как правило, у компании есть два вида используемого капитала — собственный и заемный. Собственный капитал равен сумме средств, принадлежащих самой компании или причитающихся ее акционерам. Заемный капитал — это средства, привлеченные компанией извне (кредиты и займы). Заемный капитал достается компании не бесплатно — по кредитам и займам она должна платить проценты.
В случае когда у компании или у инвестора только заемные деньги, то для них самым главным становится то, чтобы инвестиционные проекты приносили больше, чем приходится платить по кредиту. В этом случае при оценке инвестиционных проектов в качестве ставки дисконтирования можно использовать ставку по кредиту, скорректированную на ставку налога на прибыль.
Но когда у компании есть и собственный, и заемный капитал, то ставка дисконтирования по модели WACC считается следующим образом:
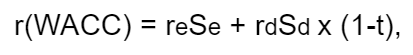
где r e — стоимость собственного капитала,
S e — доля собственного капитала,
r d — стоимость заемного капитала,
S d — доля заемного капитала,
t — ставка налога на прибыль.
Стоимость заемного капитала r d — это средневзвешенный процент по имеющимся займам и кредитам.
Стоимость собственного капитала r e может определяться либо методом CAPM, описанным выше, либо другим способом — например, с помощью модели Гордона.
Модель Гордона для оценки стоимости собственного капитала компании предполагает, что за возможность использования собственного капитала компания платит дивидендами. Значит, стоимость собственного капитала определяется отношением суммы выплаченных дивидендов к сумме денег, привлеченных в ходе размещения акций.
В итоге формула, по которой рассчитывается стоимость собственного капитала по Гордону, выглядит так:
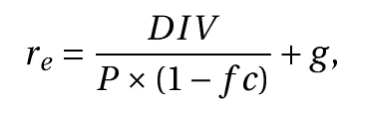
где DIV — это сумма годовых ожидаемых дивидендов на одну акцию;
P — цена размещения акций,
fc — затраты на эмиссию (в %),
g — темпы прироста дивидендов.
Мультипликативные методы — это способы расчета ставки дисконтирования на основе различных коэффициентов прироста и других коэффициентов предприятий.
Это может быть, например:
- расчет ставки на основе рентабельности капитала (ROE), когда за ставку дисконтирования принимают показатель ROE;
- расчет ставки на основе рентабельности активов (ROA), когда за ставку дисконтирования принимают показатель ROA;
- расчет ставки на основе рыночных мультипликаторов, когда за ставку дисконтирования принимают значение доходности как отношения прогнозного дохода к текущей рыночной стоимости компании. Например, прогнозное значение чистой прибыли на акцию (EPS) к рыночной стоимости акций или прогнозное значение денежного потока к капитализации

Как применяется ставка дисконтирования
Как мы писали вначале, ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.
Дисконтирование — это приведение будущей стоимости денежных потоков к стоимости в настоящее время по ставке дисконтирования.
Один из частых результатов дисконтирования — получение чистой текущей (приведенной) стоимости денег.
Чистая текущая стоимость (NPV, Net Present Value) — разница между всеми денежными притоками и оттоками, приведенными к текущему моменту времени по ставке дисконтирования. Эта величина показывает сумму денежных средств, которую инвестор ожидает получить от проекта, пересчитанную к настоящему времени.
Сравнив NPV разных по длительности инвестиционных вариантов, инвестор может выбрать наиболее доходный.
Узнайте о возможностях нашего Каталога в телеграм-канале «РБК Инвестиций»
Долговая ценная бумага, владелец которой имеет право получить от выпустившего облигацию лица, ее номинальную стоимость в оговоренный срок. Помимо этого облигация предполагает право владельца получать процент от ее номинальной стоимости либо иные имущественные права. Облигации являются эквивалентом займа и по своему принципу схожи с процессом кредитования. Выпускать облигации могут как государства, так и частные компании.
Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч.1
Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?
Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?
Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.
Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.

#1. Временная стоимость денег. Типы начисления процентов
Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.
На картинке ниже показан список фильмов с максимальными кассовыми сборами.

Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?
Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.
Итак, деньги имеют стоимость, потому что их владелец хочет компенсации за то, что он не может купить какой-то товар или услугу, и за риск, который он несет, давая деньги в долг.
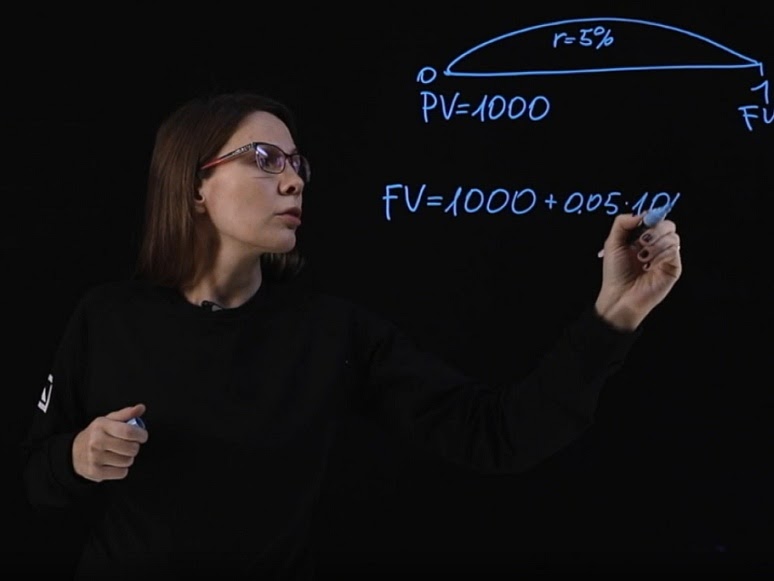
На языке математики это будет выглядеть так:
Сейчас вы мне даете тысячу рублей. Обозначим это как PV (Present Value) . Допустим ставка (r) равна 5%, и деньги вы даете мне сроком на один год. Тогда возвращая деньги FV (Future Value) , мне придется добавить к исходной сумме 50 рублей.
Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.

А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.
Простые проценты
Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.

Результат – текущее значение, умноженное на сумму единица плюс процентная ставка (r) , умноженная на число лет вклада (T) . Такой способ начисления процентов называется простыми процентами.
Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:
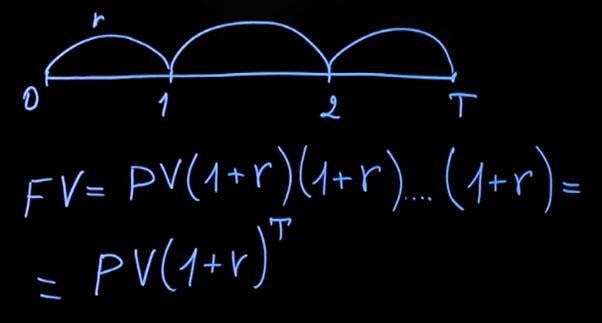
Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.
Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.
Непрерывное начисление процентов
Давайте рассмотрим, как будет выглядеть формула для начислений процентов чаще одного раза в год. В этом случае будущее значение будет равняться текущему значению, умноженному на сумму единица плюс годовая процентная ставка, деленная на количество периодов начислений в году (n) в степени nT . Если начисления производятся каждые полгода, то n=2 , если каждый день, то n=365 .

Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:
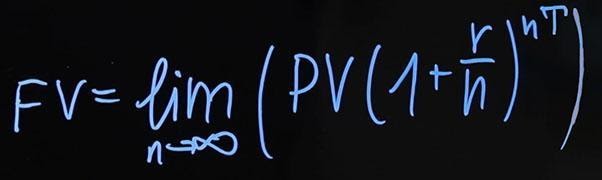
Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:
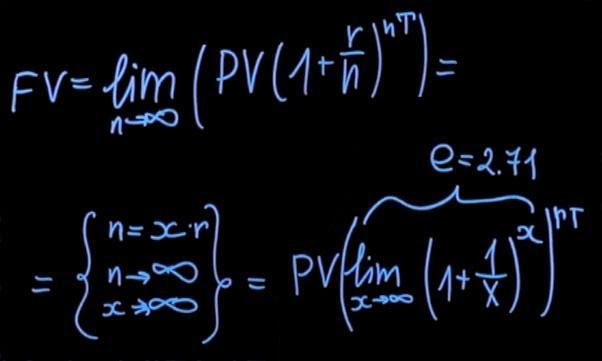
С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.

Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.
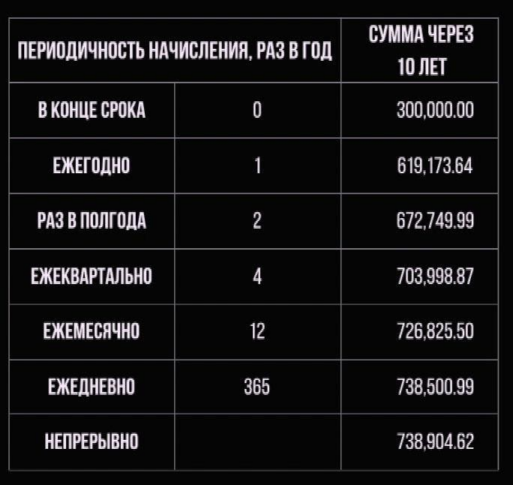
Как вы можете видеть – 300 тысяч рублей вкладчик получит в случае, если начисления производятся в конце срока действия вклада.
Таким образом сумма вклада при начислении процентов ежегодно в два раза превышает сумму вклада при выплате процентов единожды в конце срока.
Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.
На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.
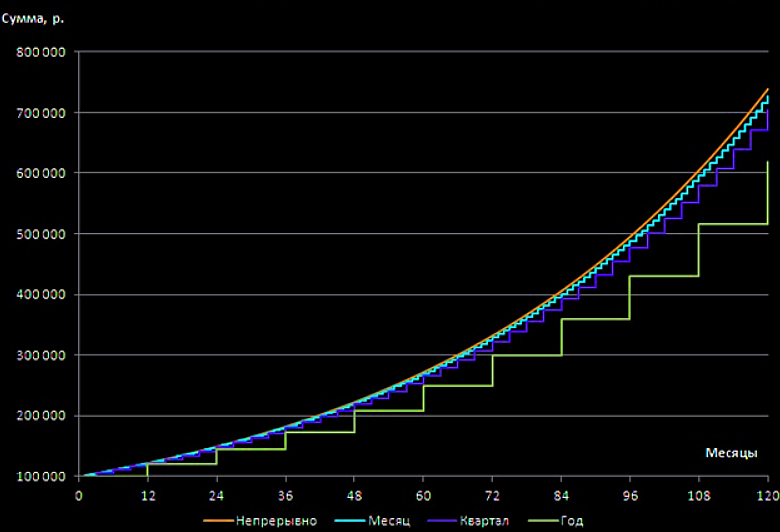
Отсюда необходимо сделать вывод:
выбирая вклад, важно смотреть не только на размер процентной ставки, но и на периодичность начисления процентов. Высокая процентная ставка не всегда является по-настоящему выгодной.
Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.
#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)
Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.
Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?
Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.

Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:
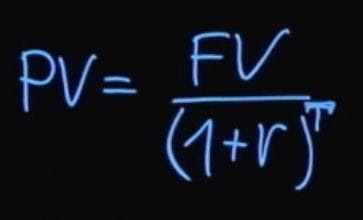
T – это количество периодов выплат начислений процентной ставки. Такой процесс деления будущего значения на единицу плюс процентная ставка в степени T называется дисконтированием. А множитель, единица деленная на сумму единицы плюс r в степени T , называется коэффициентом дисконтирования.
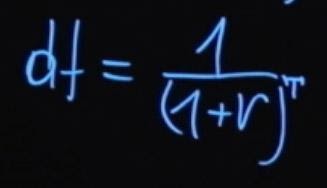
Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.
Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.
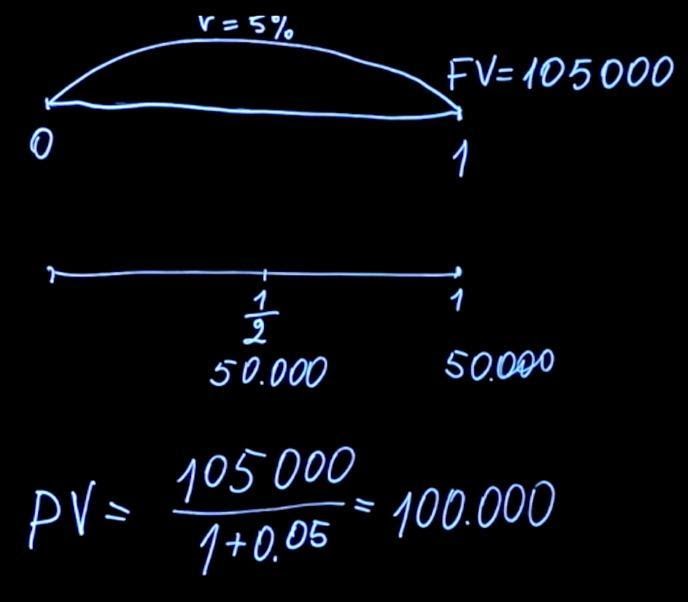
Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.
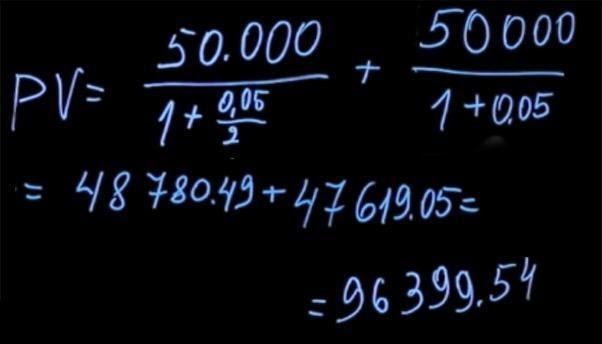
Очевидно, что предложение получить 105 тысяч рублей через год выгоднее, чем получать по 50 тысяч раз в полгода. Хотя интуитивно вам могло показаться, что разница несущественна, при том, что деньги вы получите быстрее. Математика говорит нам о том, что это не так.
Например, когда вам предлагают купить автомобиль в рассрочку или заплатить полную сумму сейчас с какой-нибудь скидкой. Нужно взять будущую сумму, которую вы заплатите, привести к текущему значению, а затем сравнивать платежи, происходящие в один и тот же момент времени.
В таком случае сравнение будет корректным.
#3. Форвардные процентные ставки
Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.

Мы находимся сейчас в моменте времени «ноль». Через год я у вас по ставке x возьму деньги и верну их вам через два года. Как рассчитать ставку x ? У нас есть несколько опций. Вы можете сейчас положить деньги по ставке r 1 на год, а затем реинвестировать их по ставке x .

Либо положить деньги сразу по ставке r 2 на два года.
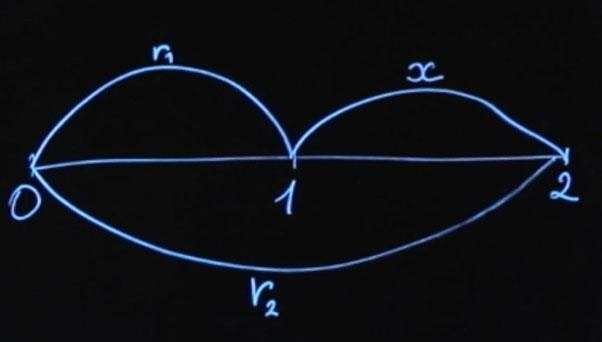
На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV 1 будет равняться текущему значению, умноженному на сумму единицы и rT 1 (будем считать, что у нас простое начисление процентов).
Момент времени T 1 у нас равняется одному году. Дальше у нас произойдет реинвестирование суммы, и мы положим на промежуток времени от T 2— T 1, умноженную на нашу процентную ставку x . T 2 – это момент времени, в нашем случае два года.
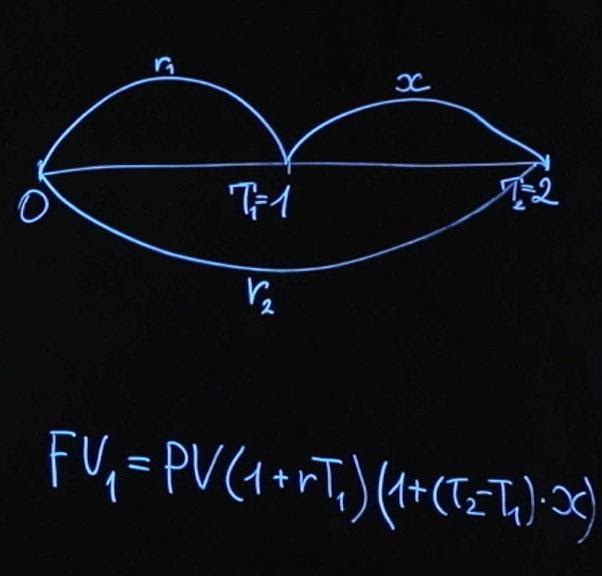
Либо будущее значение FV 2 будет равняться текущему значению PV , умноженному на единица плюс r 2, умноженное на T 2. Согласно условию отсутствия арбитража FV 1 должно равняться FV 2.
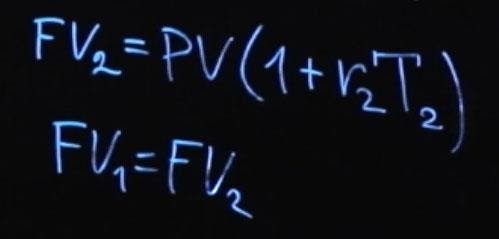
Из этого мы получаем следующее:
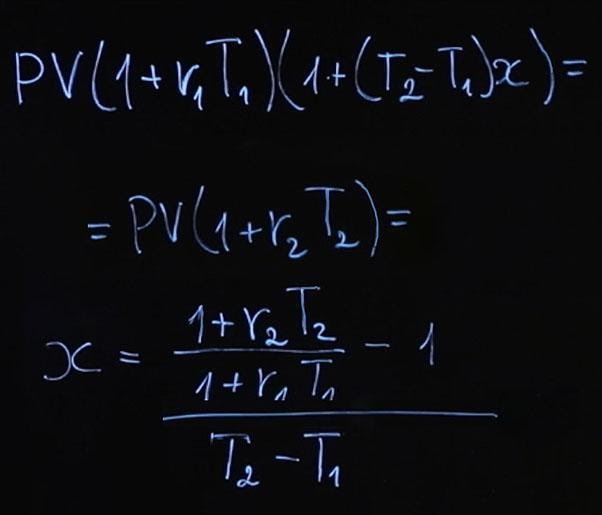
Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.
Пусть процентные ставки у нас r 1=4%; r 2=6%. В таком случае имеем следующее:
Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.
Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов ( FV=PVe rT ), то тогда мы можем переписать условие отсутствия арбитража следующим образом:
Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:
Далее легко найти x:
Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.
Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?
Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.
Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T1. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.
Источник https://nalog-nalog.ru/analiz_hozyajstvennoj_deyatelnosti_ahd/kak_rasschitat_chistyj_diskontirovannyj_dohod_formula/
Источник https://quote.rbc.ru/news/article/6283b0189a79470998b95e63
Источник https://habr.com/ru/company/dbtc/blog/501566/





